Linear regression
What does linear regression do?
- fit a straight line to two-dimensional data: \(y_i = \alpha + \beta \cdot x_i + \epsilon_i\)
- (so that the sum of squared errors is minimized)
- \(\epsilon_i \sim N(0, \sigma)\) - normally distributed with same \(\sigma\)
- `linear-’ refers to the regression coefficients \(\alpha\) and \(\beta\), nonlinear functions in \(x\) can be fitted!
- function:
lm()(and others)
Assumptions
- equal variance assumption (homoscledasticity): same \(\sigma\) for all \(\epsilon_i\)
- residuals \(\epsilon_i\) normally distributed (if significance tests are being considered)
- residulas \(\epsilon_i\) independent
- a matter of course: plot should look linearly (always plot first!)
Linear regression using lm()
Some data
x = seq(1:12)
y = 2*x + rnorm(length(x), mean = 0, sd = 1.5) # linear, with some noise
plot(x, y, main = "Measurements", font.main = 1)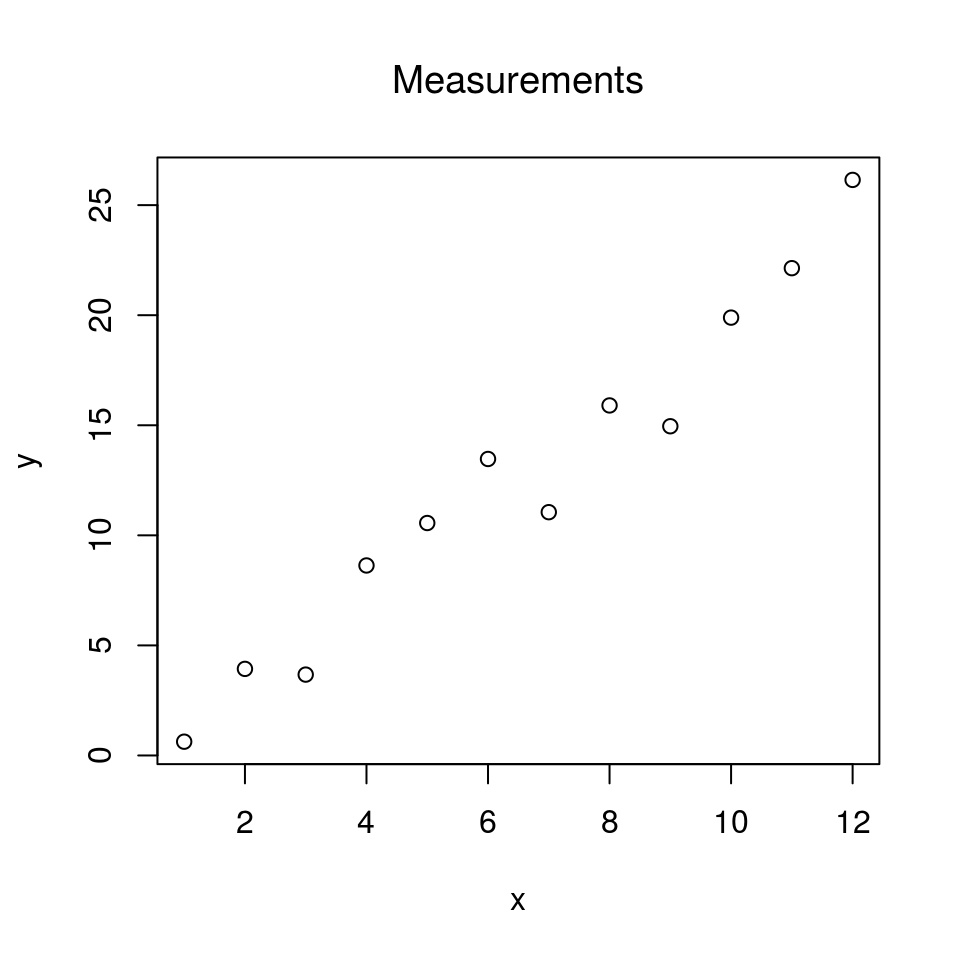
If the plot looks fairly linear, a linear regression can be conducted:
# create data frame first
dat = data.frame(x = x, y = y)
class(dat)## [1] "data.frame"head(dat)## x y
## 1 1 0.6250132
## 2 2 3.9321971
## 3 3 3.6727819
## 4 4 8.6304480
## 5 5 10.5587800
## 6 6 13.4679846# run lm():
lm.out <- lm(y ~ x, data = dat)
summary(lm.out)##
## Call:
## lm(formula = y ~ x, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.8996 -0.6461 0.1094 1.1879 1.9630
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.1312 1.0474 -1.08 0.306
## x 2.1095 0.1423 14.82 3.92e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.702 on 10 degrees of freedom
## Multiple R-squared: 0.9565, Adjusted R-squared: 0.9521
## F-statistic: 219.7 on 1 and 10 DF, p-value: 3.921e-08Reading the output
- Coefficients/Estimates displays the calculated values for \(\alpha\) and \(\beta\)
- \(\alpha = -0.9850\)
- \(\beta = 2.1124\) (the estimated slope)
- note that the estimated slope is close to the true slope, which is 2.
- Coefficients/Pr(>|t|) are the p-values for the T-test
- \(H_0: \; \beta = 0\)
- if the p-value for \(\beta\) is low, the \(H_0\) is rejected, i.e. the slope is significantly different from 0.
R squared (coefficient of determination) describes how good the fit is. A value close to 1 is good.
The p-value for the F statistic should be small. That means that the fit makes sense.
Draw the regression line using the lm() results
# str(lm.out)
alpha = lm.out$coefficients[1]
beta = lm.out$coefficients[2]
plot(x, y)
abline(a = alpha, b = beta, col = "red")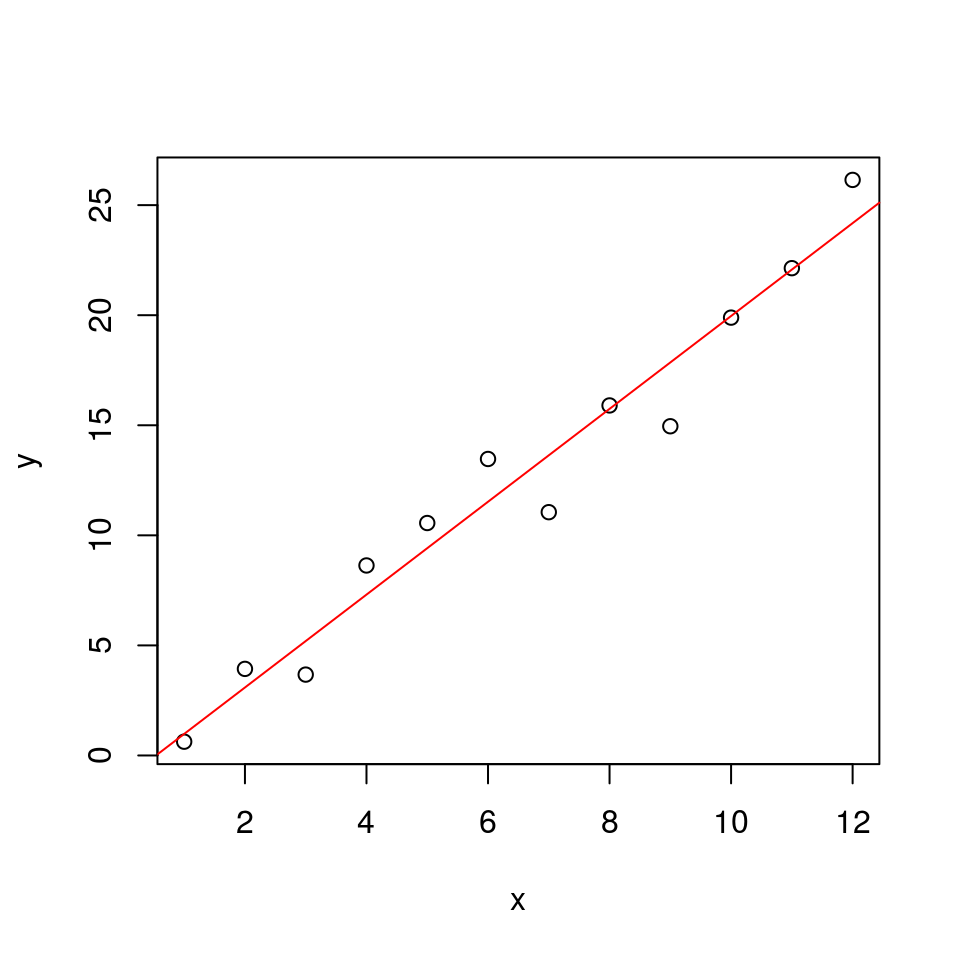
Checking if the assumptions were fullfilled
Yes!, this is done afterwards
Check homoscedasticity and normality:
# plot(lm.out)
residuals = resid(lm.out)
par(mfrow = c(1, 2))
plot(residuals, col = "blue", main = "Residuals")
abline(h = 0, col = "red", lty = 2)
qqnorm(residuals, col = "blue")
qqline(residuals, col = "red", lty = 2)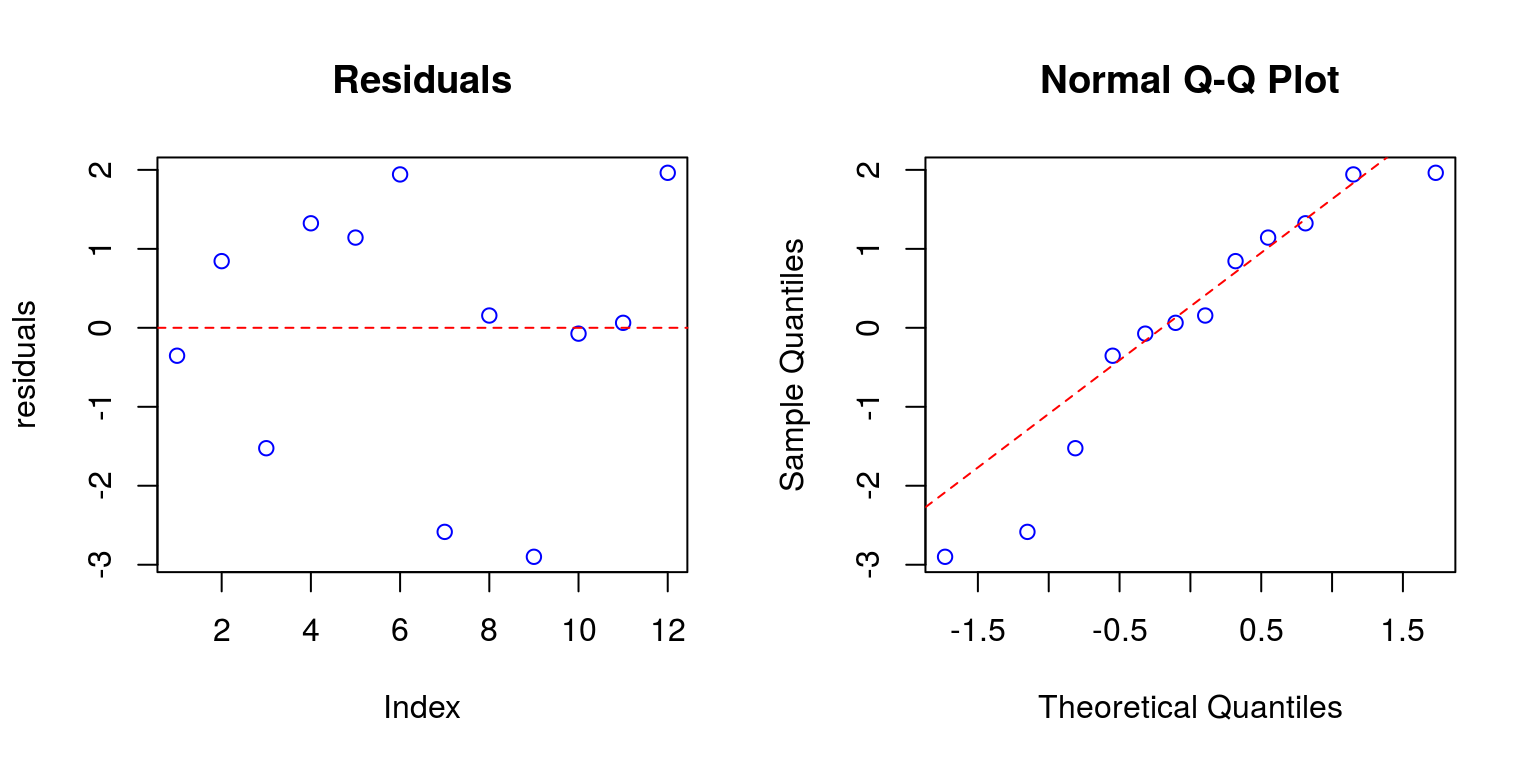
par(mfrow = c(1, 1))Independence of the residuals can be checked using an autocorrelation plot
auto.cor = acf(resid(lm.out))
plot(auto.cor)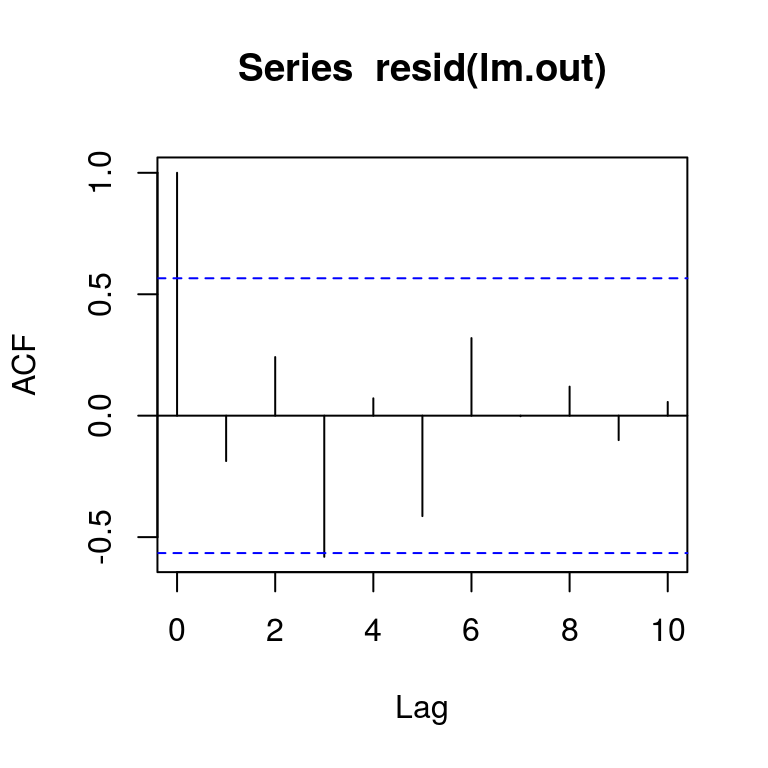
Why is plotting necessary?
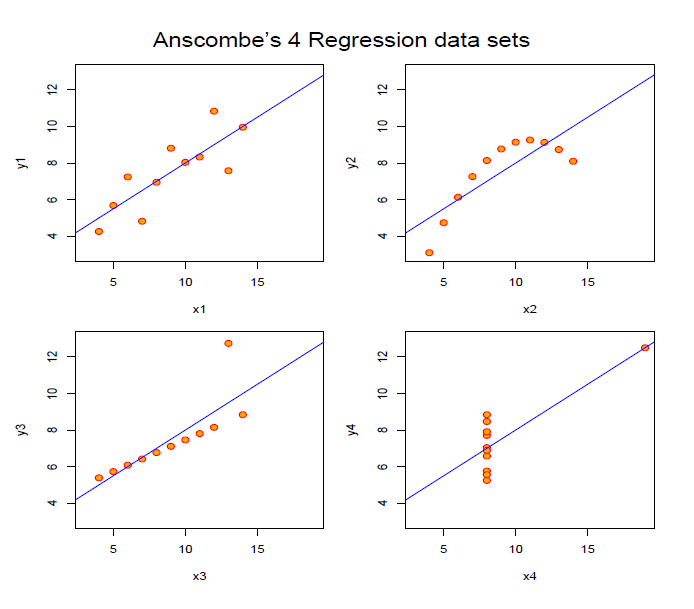
Technically, lm() will work in most of the cases. But all datasets above yield the same regression line!
Non-linear dependency on x
No problem!
set.seed(777)
x = seq(1:12)
y = x^2 + rnorm(length(x), mean = 0, sd = 1.9)
plot(x, y)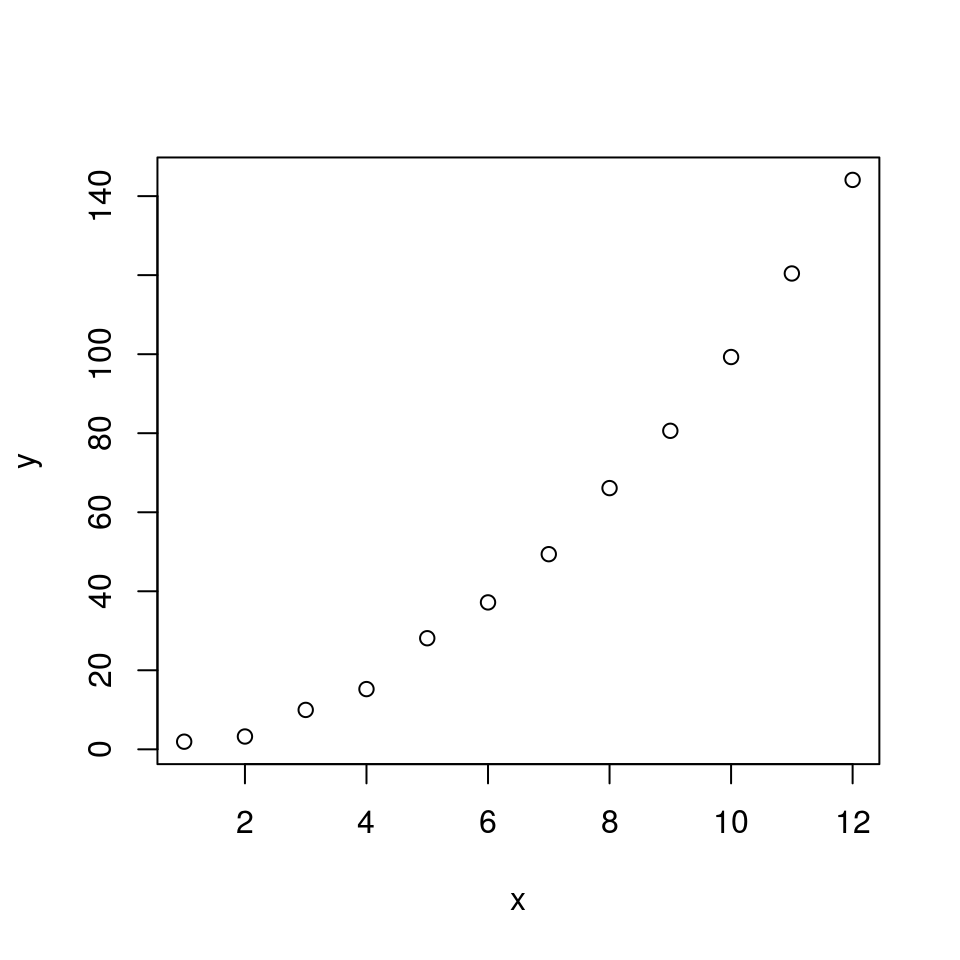
It would be possible to define a new variable \(\acute{x} = x^2\) and to feed the lm() with this variable.
However, it is probably easier to use Wilkinson-Rogers (W-R) notation:
dat2 = data.frame(y = y, x = x)
lm.out = lm(y ~ I(x^2), data = dat2)
summary(lm.out)##
## Call:
## lm(formula = y ~ I(x^2), data = dat2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.60202 -0.70048 -0.02812 0.38199 2.42752
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.875034 0.556126 1.573 0.147
## I(x^2) 0.992438 0.007819 126.932 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.249 on 10 degrees of freedom
## Multiple R-squared: 0.9994, Adjusted R-squared: 0.9993
## F-statistic: 1.611e+04 on 1 and 10 DF, p-value: < 2.2e-16Draw the regression line using the lm() results
# str(lm.out)
alpha = lm.out$coefficients[1]
beta = lm.out$coefficients[2]
plot(x, y)
lines(alpha + beta*x^2, col = "red") 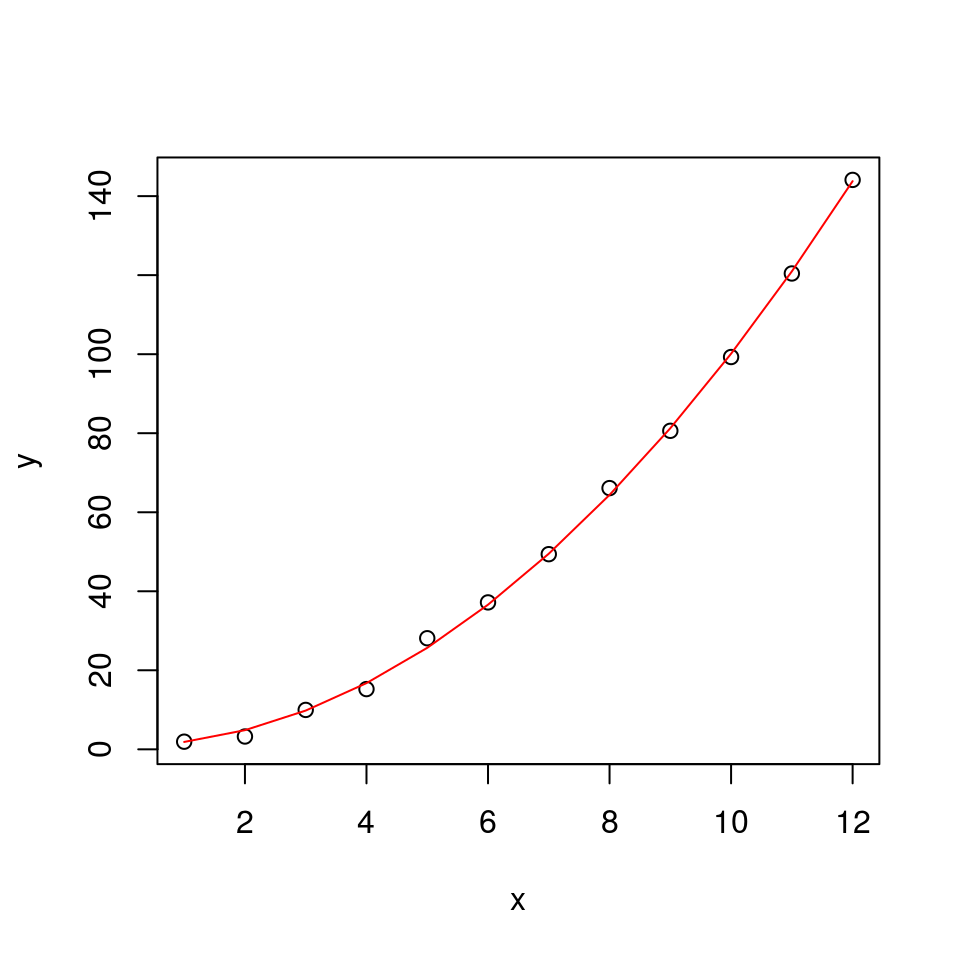
More possibilities
- y ~ poly(x, …) (Polynom fitting)
- lm(log(y) ~ x) (Regression on transformed data)
- res = model(y ~ x); boxcox(res) ( Find power of y that improves the fit; library(MASS) )